（本小题满分14分）如图所示，某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地，并考
虑与周边环境协调，设计要求该图书馆底面矩形的四个顶点都要在边界上，图书馆的正
面要朝市政府大楼.设扇形的半径OM＝R ，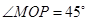
，OB与OM之间的夹角为
.
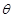（1）将图书馆底面矩形ABCD的面积S表示成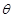的函数.
（2）若 R＝45 m，求当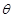为何值时，矩形ABCD的面积S有最大值？
其最大值是多少？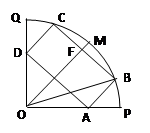
（本小题满分12分）
已知椭圆
的左、右焦点为
、
，上顶点为A，直线
交椭圆于
. 如图所示沿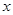
轴折起，使得平面
平面
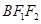. 点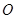
为坐标原点.
( I ) 求三棱锥
的体积；
（Ⅱ）线段
上是否存在点
，使得
，若存在，请在图1中指出点的坐标；若不存在，请说明理由.
（本小题满分12分）
如图，从点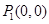
做x轴的垂线交曲线
于点
曲线在
点处的切线与x轴交于点
，再从做x轴的垂线交曲线于点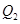
，依次重复上述过程得到一系列点：
记
，
.
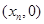（Ⅰ）求点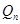
处的切线方程，并指出
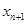与
的关系；
（Ⅱ）求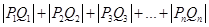
(本小题满分12分）
如图，圆
:
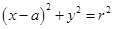
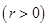与抛物线
：
的一个交点M
，且抛物线在点M处的切线过圆心. 
（Ⅰ）求和的标准方程；
（Ⅱ）若点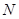
为抛物线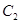
上的一动点，求
的取值范围．
（本小题满分12分）
某园林局对1000株树木的生长情况进行调查，其中杉树 600株，槐树400株 .现用分层抽样方法从这1000株树木中随机抽取100株，杉树与槐树的树干周长（单位：cm）的抽查结果如下表：
| 树干周长 （单位：cm ） |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
| 杉树 |
6 |
19 |
21 |
 |
| 槐树 |
4 |
20 |
 |
6 |
(I)求，值及估计槐树树干周长的众数；
（Ⅱ）如果杉树的树干周长超过60cm就可以砍伐，请估计该片园林可以砍伐的杉树有多少株？
（Ⅲ）树干周长在30cm到40cm之间的4株槐树有1株患虫害，现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
（本小题满分12分）
如图某河段的两岸可视为平行，为了测量该河段的宽度，在河段的一岸边选取两点A、B，观察对岸的点C,测得
，
,且
米.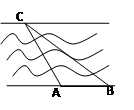
（1）求
；
（2）求该河段的宽度.