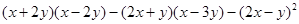随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场。一水果经销商购进了A，B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售。预计每箱水果的盈利情况如下表：
有两种配货方案（整箱配货）：
方案一：甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；
方案二：按照甲、乙两店盈利相同配货，其中A种水果甲店_________箱，乙店__________箱；B种水果甲店_________箱，乙店__________箱.如果按照方案一配货，请你计算出经销商能盈利多少元？
请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多？
在甲、乙两店各配货10箱，且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？
如图，已知A(n，-2)，B(1，4)是一次函数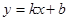
的图象和反比例函数y=
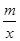的图象的两个交点，直线AB与y轴交于点C．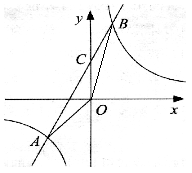
(1)求反比例函数和一次函数的关系式；
(2)求△AOB的面积；
(3)求不等式
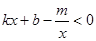的解集(直接写出答案)．
设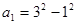
，
，
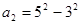……（1）写出
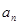（n为大于0的自然数）的表达式；（2）探究
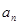是否为8的倍数，并用文字语言表述你所获得的结论；（3）若一个数的算术平方根是一个自然数，则这个数是“完全平方数”，试找出
，
，
，……，
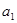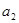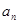这一列数中从小到大排列的前4个完全平方数；并说出当
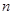满足什么条件时, 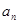为完全平方数(不必说明理由).
某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：
信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；
信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．
根据以上信息，原来报名参加的学生有多少人？
已知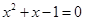
，求
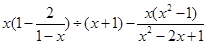的值．
计算：