(12分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上 大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是
大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是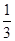 ,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
(1) 求该学生考上大学的概率;
求该学生考上大学的概率;
(2)如果考上大学或参加完5次考试就结束,求该生至少参加四次考试的概率.
(本小题满分13分)设函数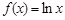 ,
, ,函数
,函数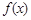 的图象与
的图象与 轴的交点在函数
轴的交点在函数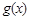 的图象上,且在此点处两曲线有相同的切线.
的图象上,且在此点处两曲线有相同的切线.
(Ⅰ) 求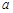 、
、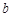 的值;
的值;
(Ⅱ) 设定义在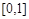 上的函数
上的函数 的最大值为
的最大值为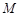 ,最小值为
,最小值为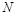 ,且
,且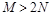 ,求实数
,求实数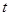 的取值范围.
的取值范围.
(本小题满分12分)已知数列 的前
的前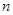 项和为
项和为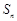 ,
,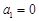 ,
,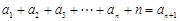 ,
,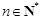 .
.
(Ⅰ) 求证:数列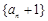 是等比数列;
是等比数列;
(Ⅱ) 设数列 的前
的前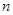 项和为
项和为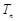 ,
,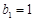 ,点
,点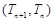 在直线
在直线 上,若不等式
上,若不等式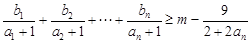 对于
对于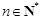 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(本小题满分12分)如图,在多面体 中,底面
中,底面 是边长为
是边长为 的的菱形,
的的菱形,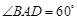 ,四边形
,四边形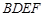 是矩形,平面
是矩形,平面 平面
平面 ,
,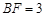 ,
, 和
和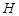 分别是
分别是 和
和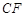 的中点.
的中点.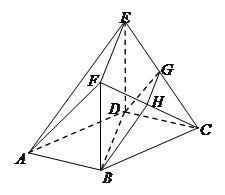
(Ⅰ)求证:平面 平面
平面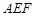 ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分12分)某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为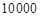 元,此鱼的市场价格和鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
元,此鱼的市场价格和鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
鱼池产量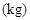 |
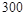 |
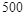 |
| 概 率 |
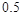 |
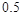 |
鱼的市场价格(元/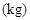 |
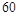 |
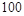 |
| 概 率 |
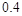 |
 |
(Ⅰ)设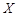 表示在这个鱼池养殖
表示在这个鱼池养殖 季这种鱼的利润,求
季这种鱼的利润,求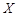 的分布列和期望;
的分布列和期望;
(Ⅱ)若在这个鱼池中连续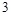 季养殖这种鱼,求这
季养殖这种鱼,求这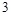 季中至少有
季中至少有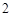 季的利润不少于
季的利润不少于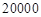 元的概率.
元的概率.
(本小题满分12分)已知函数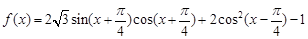 ,
, .
.
(Ⅰ)若函数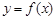 的图象关于直线
的图象关于直线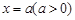 对称,求
对称,求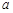 的最小值;
的最小值;
(Ⅱ)若函数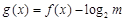 在
在 上有零点,求实数
上有零点,求实数 的取值范围.
的取值范围.