（本小题满分12分）某鱼类养殖户在一个鱼池中养殖一种鱼，每季养殖成本为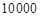
元，此鱼的市场价格和鱼池的产量均具有随机性，且互不影响，其具体情况如下表：
鱼池产量 |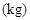
 |
 |
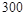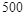| 概 率 |
 |
|
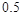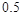| 鱼的市场价格（元/ |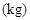
 |
 |
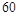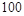| 概 率 |
 |
 |
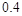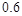（Ⅰ）设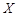
表示在这个鱼池养殖
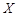季这种鱼的利润，求的分布列和期望；
（Ⅱ）若在这个鱼池中连续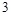
季养殖这种鱼，求这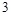季中至少有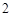
季的利润不少于
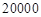元的概率．
(10分)已知圆C与圆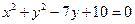
相交，所得公共弦平行于已知直线
，又圆C经过点A（-2，3），B（1，4），求圆C的方程。
(10分)△ABC中，已知三个顶点的坐标分别是A（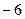
，0），B（6，0），C（6，5），
（1）求AC边上的高线BH所在的直线方程；
（2）求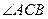
的角平分线所在直线的方程。
（本小题满分12分）设递增等比数列{
}的前n项和为
，且
＝3，
＝13，数列{
}满足
＝
，点P（，
）在直线x－y＋2＝0上，n∈N﹡
（Ⅰ）求数列{
}，{}的通项公式
（Ⅱ）设
＝
，数列{}的前n项和
，若>2a－1恒成立（n∈N﹡），求实数a的取值范围．
（本小题满分12分）
已知半圆x2＋y2＝3（y≥0），P为半圆上任一点，A（2，0）为定点，以P
A为边作正三角形PAB，且点B与圆心分别在PA的两侧，求四边形POAB面积的最大值．
（本小题满分12分）
解不等式x2－x＋a－a2<0．