A处一缉私艇发现在北偏东45°方向，距离12 n mile的海面C处有一走私船正以10 n mile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为14 n mile/h，若要在最短的时间内追上该走私船，缉私艇应沿北偏东45°+α的方向去追，求追击所需的时间和α角的正弦值.
（本小题满分12分）已知函数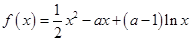
，其中
，讨论函数
的单调性.
（本小题满分12分）已知函数
，过点
作曲线
的切线的方程，求切线方程．
（文）．已知圆
及点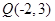
．
（1）
在圆上，求线段
的长及直线的斜率；
（2）若
为圆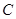
上任一点，求
的最大值和最小值；
（3）若实数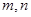
满足
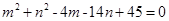,求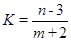
的最大值和最小值．
如图7,.已知圆O：
和定点A(2,1)，
由圆O外一点
向圆O引切线PQ，切点为Q，且满足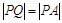
．(1) 求实数a、b间满足的等量关系；
(2) 求线段PQ长的最小值；(3) 若以P为圆心所作的圆P与圆O有公共点，试求半径取最小值时圆P的方程．
已知圆C：x2+y2-2x+4y-4=0,问是否存在斜率是1的直线l，使l被圆C截得的弦AB，以AB为直径的圆经过原点，若存在，写出直线l的方程；若不存在，说明理由.