如图7,.已知圆O: 和定点A(2,1),
和定点A(2,1),
由圆O外一点 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足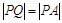 .(1) 求实数a、b间满足的等量关系;
.(1) 求实数a、b间满足的等量关系;
(2) 求线段PQ长的最小值;(3) 若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
已知 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中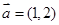
(1)若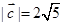 ,且
,且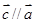 ,求:
,求: 的坐标
的坐标
(2)若 ,且
,且 与
与 垂直,求
垂直,求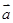 与
与 的夹角
的夹角
已知椭圆 过点
过点 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点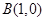 且斜率为
且斜率为 (
(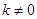 )的直线
)的直线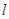 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线 、
、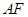 分别交直线
分别交直线 于
于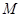 、
、 两点,线段
两点,线段 的中点为
的中点为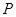 .记直线
.记直线 的斜率为
的斜率为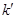 ,求证:
,求证:  为定值.
为定值.
设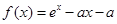 .
.
(Ⅰ)若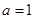 ,求
,求 的单调区间;
的单调区间;
(Ⅱ) 若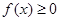 对一切
对一切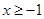 恒成立,求
恒成立,求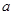 的取值范围.
的取值范围.
如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中点,F是AB中点,AC = 1,BC = 2,AA1 = 4.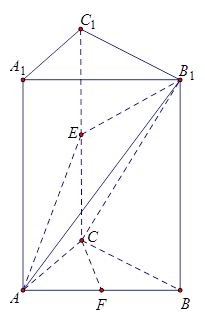
(1)求证:CF∥平面AEB1;(2)求三棱锥C-AB1E的体积.
设函数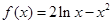 .(I)求函数
.(I)求函数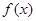 的单调递增区间;
的单调递增区间;
(II) 若关于 的方程
的方程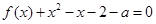 在区间
在区间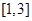 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数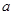 的取值范围.
的取值范围.