已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2, ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为α,β,且α+β=π,试问直线l是否过定点?若过,求该定点的坐标.
已知函数 ,
, ,若函数
,若函数 在
在 处的切线方程为
处的切线方程为 ,
,
(1)求 的值;
的值;
(2)求函数 的单调区间。
的单调区间。
延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
| 月收入(元) |
[1000,2000) |
[2000,3000) |
[3000,4000) |
[4000,5000) |
[5000,6000) |
[6000,7000) |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 反对人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据估算月收入高于4000的调查对象中,持反对态度的概率;
(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为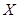 ,求
,求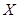 的分布列和数学期望.
的分布列和数学期望.
已知函数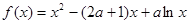
(1) 当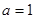 时, 求函数
时, 求函数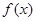 的单调增区间;
的单调增区间;
(2)当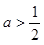 时,求函数
时,求函数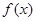 在区间
在区间 上的最小值;
上的最小值;
已知函数 ,其中
,其中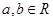
(1)若曲线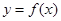 在点
在点 处的切线方程为
处的切线方程为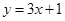 ,求函数
,求函数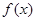 的解析式;
的解析式;
(2)讨论函数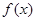 的单调区间;
的单调区间;
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点
,点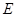 在棱
在棱 上.
上.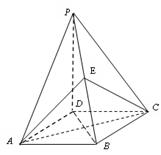
(Ⅰ) 求证:平面 平面
平面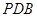 ;
;
(Ⅱ) 当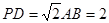 ,且
,且 时,确定点
时,确定点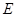 的位置,即求出
的位置,即求出 的值.
的值.