已知函数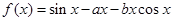
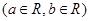 .
.
(1)若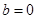 ,讨论函数
,讨论函数 在区间
在区间 上的单调性;
上的单调性;
(2)若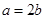 且对任意的
且对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知椭圆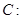
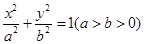 的左焦点为
的左焦点为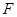 ,左、右顶点分别为
,左、右顶点分别为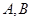 ,过点
,过点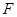 且倾斜角为
且倾斜角为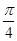 的直线
的直线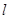 交椭圆于
交椭圆于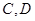 两点,椭圆
两点,椭圆 的离心率为
的离心率为 ,
,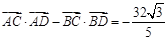 .
.
(1)求椭圆 的方程;
的方程;
(2)若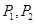 是椭圆上不同两点,
是椭圆上不同两点,
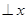 轴,圆
轴,圆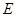 过点
过点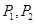 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆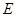 内,则称圆
内,则称圆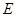 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆 是否存在过点
是否存在过点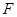 的内切圆?若存在,求出点
的内切圆?若存在,求出点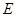 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,已知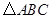 中,
中,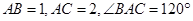 ,点
,点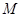 是边
是边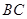 上的动点,动点
上的动点,动点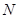 满足
满足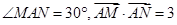 (点
(点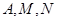 按逆时针方向排列).
按逆时针方向排列).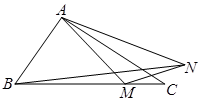
(1)若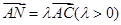 ,求
,求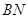 的长;
的长;
(2)求△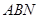 面积的最大值.
面积的最大值.
如图,已知正方形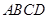 的边长为
的边长为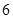 ,点
,点 分别在边
分别在边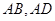 上,
上, ,现将△
,现将△ 沿线段
沿线段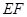 折起到△
折起到△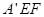 位置,使得
位置,使得 .
.
(1)求五棱锥 的体积;
的体积;
(2)求平面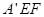 与平面
与平面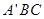 的夹角.
的夹角.
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
 |
| 甲 |
3 |
7 |
20 |
40 |
20 |
10 |
| 乙 |
5 |
15 |
35 |
35 |
7 |
3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.