如果实数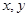 满足
满足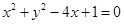 ,求①
,求①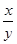 的最大值;②
的最大值;②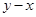 的最小值;
的最小值;
③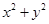 的最值.
的最值.
已知极坐标的极点与平面直角坐标系的原点重合,极轴与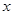 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆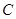 的参数方程为
的参数方程为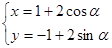 (
( 为参数),点
为参数),点 的极坐标为
的极坐标为 .(Ⅰ)化圆
.(Ⅰ)化圆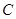 的参数方程为极坐标方程;(Ⅱ)若点
的参数方程为极坐标方程;(Ⅱ)若点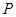 是圆
是圆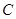 上的任意一点, 求
上的任意一点, 求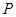 ,
, 两点间距离的最小值.
两点间距离的最小值.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若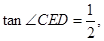 ⊙O的半径为3,求OA的长.
⊙O的半径为3,求OA的长.
已知函数 ,其中常数
,其中常数 .
.
(Ⅰ)当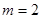 时,求
时,求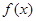 的极大值;(Ⅱ)试讨论
的极大值;(Ⅱ)试讨论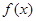 在区间
在区间 上的单调性;
上的单调性;
(3)当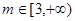 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 ,
, ,使曲线
,使曲线 在点
在点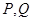 处的切线互相平行,求
处的切线互相平行,求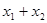 的取值范围.
的取值范围.
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(Ⅰ)若∠APB=60°,试求点P的坐标;
(Ⅱ)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=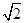 时,求直线CD的方程.
时,求直线CD的方程.
已知sin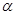 +cos
+cos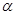 =
= ,
,
求 的值.
的值.