如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a, ,种草的面积为
,种草的面积为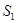 ,种花的面积为
,种花的面积为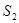 ,比值
,比值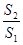 称为“规划和谐度”。
称为“规划和谐度”。
(I)试用 表示
表示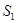 ,
,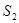 ;
;
(II)若 为定值,BC >AB。当
为定值,BC >AB。当 为何值时,“规划和谐度”有最小值?最小值是多少?
为何值时,“规划和谐度”有最小值?最小值是多少?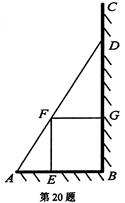
如图所示,某市政府决定在以政府大楼 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径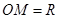 ,
,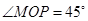 ,
,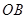 与
与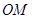 之间的夹角为
之间的夹角为 .
.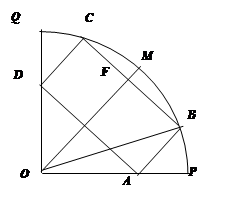
(1)将图书馆底面矩形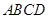 的面积
的面积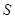 表示成
表示成 的函数.
的函数.
(2)求当 为何值时,矩形
为何值时,矩形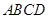 的面积
的面积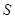 有最大值?
有最大值?
(3)其最大值是多少?(用含R的式子表示)
如图,已知空间四边形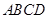 中,
中,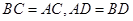 ,
, 是
是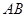 的中点.
的中点.
求证:(1)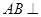 平面CDE;
平面CDE;
(2)平面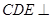 平面
平面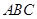
(3)若G为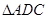 的重心,试在线段AE上确定一点F, 使得GF//平面CDE.
的重心,试在线段AE上确定一点F, 使得GF//平面CDE.
已知复数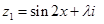 ,
,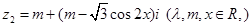 ,且
,且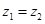 .
.
(1)若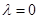 且
且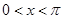
 ,求
,求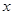 的值;
的值;
(2)设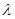 =
=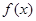 ,已知当
,已知当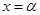 时,
时,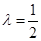 ,试求
,试求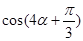 的值.
的值.
设函数 .
.
(1)解不等式
(2)若关于 的不等式
的不等式 的解集不是空集,试求实数
的解集不是空集,试求实数 的取值范围.
的取值范围.
已知曲线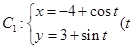 为参数),
为参数),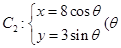 为参数).
为参数).
(1)化 的方程为普通方程
的方程为普通方程
(2)若 上的点
上的点 对应的参数为
对应的参数为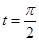 ,
,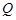 为
为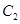 上的动点,求
上的动点,求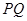 中点
中点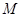 到直线
到直线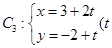 为参数)距离的最小值.
为参数)距离的最小值.