在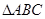 中,角
中,角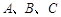 所对的边分别为
所对的边分别为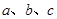 ,已知
,已知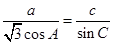 ,
,
(1)求 的大小;(2)若
的大小;(2)若 求
求 的值.
的值.
已知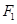 、
、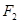 分别是椭圆
分别是椭圆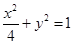 的左、右焦点.
的左、右焦点.
(1)若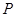 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,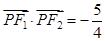 ,求点
,求点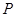 的坐标;
的坐标;
(2)设过定点 的直线
的直线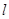 与椭圆交于不同的两点
与椭圆交于不同的两点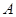 、
、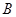 ,且
,且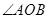 为锐角(其
为锐角(其
中 为坐标原点),求直线
为坐标原点),求直线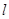 的斜率
的斜率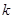 的取值范围.
的取值范围.
如图,直三棱柱(侧棱垂直于底面的棱柱) ,底面
,底面 中
中 ,棱
,棱 ,
, 分别为
分别为 的中点.
的中点.
(1)求 >的值;
>的值;
(2)求证:
已知定点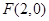 和定直线
和定直线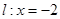 ,动点与定点
,动点与定点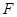 的距离等于点
的距离等于点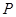 到定直线
到定直线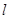 的距离,记动点
的距离,记动点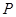 的轨迹为曲线
的轨迹为曲线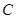 .
.
(1)求曲线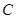 的方程.
的方程.
(2)若以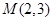 为圆心的圆与曲线
为圆心的圆与曲线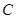 交于
交于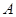 、
、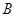 不同两点,且线段
不同两点,且线段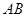 是此圆的直径时,求直线
是此圆的直径时,求直线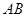 的方程.
的方程.
在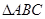 中,角
中,角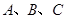 所对的边分别为
所对的边分别为 ,已知
,已知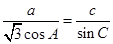 ,
,
(1)求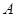 的大小;
的大小;
(2)若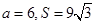 ,求
,求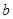 和
和 的值.
的值.