(1)(满分7分) 选修4一2:矩阵与变换
二阶矩阵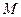 对应的变换将点
对应的变换将点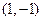 与
与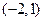 分别变换成点
分别变换成点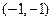 与
与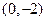 .
.
(Ⅰ)求矩阵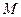 ;
;
(Ⅱ)设直线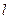 在矩阵
在矩阵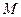 对应变换的作用下得到直线
对应变换的作用下得到直线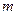 :
: 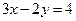 ,求
,求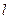 的方程.
的方程.
已知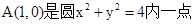 ,B、D是圆上两动点,且四边形ABCD是矩形(1)求顶点C的轨迹E的方程;
,B、D是圆上两动点,且四边形ABCD是矩形(1)求顶点C的轨迹E的方程;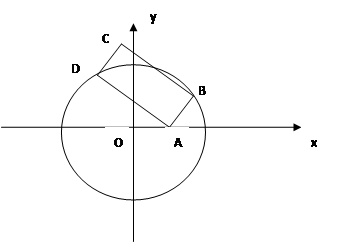
( 12分)已知正项数列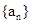 的前n项和满足
的前n项和满足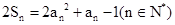
(1)求数列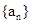 的通项公式;
的通项公式;
(2)设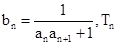 是数列
是数列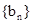 的前n项的和,求证:
的前n项的和,求证: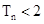
将一个各面上均涂有红色的正方体锯成27个同样大小的小正方体,
(1)从这些小正方体中任取一个,求其中至少有两个面涂有红色的概率;
(2)从中任取2个小正方体,记2个小正方体涂有红色的面数和为ξ,求ξ的分布列和数学期望.
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,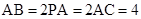 ,N为AB上一点且满足
,N为AB上一点且满足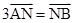 ,M,S分别为PB,BC的中点
,M,S分别为PB,BC的中点
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小;
(3)求三棱锥P-ABC外接球的体积V。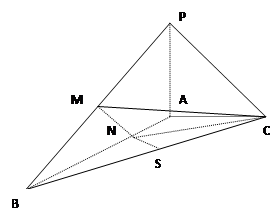
在△ABC中,边a,b,c分别对应角A、B、C,且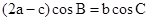
(1)求角B的值;
(2)若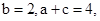 求△ABC的面积
求△ABC的面积