在“我爱祖国”演讲比赛中,学校根据初赛成绩在七,八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据上图和上表提供的信息,解答下列问题:(1)请你把上边的表格填写完整;
(2)考虑平均数与方差,你认为 年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
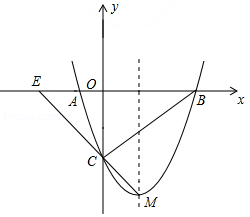
如图所示,抛物线 与 轴相交于 、 两点,与 轴相交于点 ,点 为抛物线的顶点.
(1)求点 及顶点 的坐标.
(2)若点 是第四象限内抛物线上的一个动点,连接 、 ,求 面积的最大值及此时点 的坐标.
(3)若点 是抛物线对称轴上的动点,点 是抛物线上的动点,是否存在以点 、 、 、 为顶点的四边形是平行四边形.若存在,求出点 的坐标;若不存在,试说明理由.
(4)直线 交 轴于点 ,若点 是线段 上的一个动点,是否存在以点 、 、 为顶点的三角形与 相似.若存在,求出点 的坐标;若不存在,请说明理由.
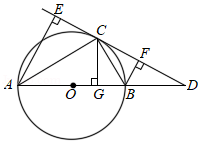
如图,在 中, 为直径,点 为圆上一点,延长 到点 ,使 ,且 .
(1)求证: 是 的切线.
(2)分别过 、 两点作直线 的垂线,垂足分别为 、 两点,过 点作 的垂线,垂足为点 .求证: .
某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.
(1)设该商店购进甲型平板电脑 台,请写出全部售出后该商店获利 与 之间函数表达式.
(2)若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.
定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形 中, , ,过点 作 垂线交 的延长线于点 ,且 ,证明:四边形 是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形 内接于 中, .求 的半径.
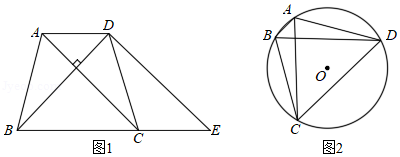
如图,某数学兴趣小组为测量一棵古树的高度,在距离古树 点处测得古树顶端 的仰角为 ,然后向古树底端 步行20米到达点 处,测得古树顶端 的仰角为 ,且点 、 、 在同一直线上,求古树 的高度.(已知: , ,结果保留整数)
