(本小题满分14分)已知椭圆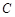 :
: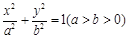 的离心率为
的离心率为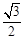 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线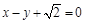 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 、
、 是椭圆
是椭圆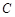 上关于
上关于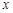 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结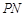 交椭圆
交椭圆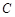 于另一点
于另一点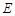 ,求直线
,求直线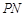 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线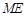 与
与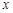 轴相交于定点.
轴相交于定点.
已知函数f(x)=xln x,g(x)=x3+ax2-x+2.
(1)求函数f(x)的单调区间;
(2)对一切x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
已知函数f(x)=2sin ωx-4sin 2 +2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
+2+a(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为2.
(1)求函数f(x)的最小正周期;
(2)若f(x)在区间[6,16]上的最大值为4,求a的值.
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
(1)当实数t为何值时,数列{an}是等比数列?
(2)在(1)的结论下,设bn=log3an+1,Tn是数列 的前n项和, 求T2 013的值.
的前n项和, 求T2 013的值.
辽宁某大学对参加全运会的志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量X,求随机变量X的分布列.
(3)求X的数学期望.
设不等式 的解集与关于
的解集与关于 的不等式
的不等式 的解集相同.
的解集相同.
(1)求 ,
,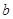 的值;
的值;
(2)求函数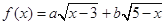 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的值.
的值.