已知圆C经过P（4，–2），Q（–1，3）两点，且在y轴上截-优题课

已知圆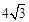C经过P（4，– 2），Q（– 1，3）两点，且在y轴上截得的线段长为，半径小于5．
（1）求直线PQ与圆C的方程．
（2）若直线l∥PQ，且l与圆C交于点A、B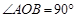，，求直线l的方程．

科目数学题型解答题难度容易

随机将 $1, 2, \dots, 2 n (n \in N^{*}, n \geq 2)$ 这 $2 n$ 个连续正整数分成 $A, B$ 两组，每组 $n$ 个数， $A$ 组最小数为 $a_{1}$ ，最大数为 $a_{2}$ ； $B$ 组最小数为 $b_{1}$ ，最大数为 $b_{2}$ ，记 $ξ = a_{2} - a_{1}, η = b_{2} - b_{1}$

（1）当 $n = 3$ 时，求 $ξ$ 的分布列和数学期望；
（2）令 $C$ 表示事件 $ξ$ 与 $η$ 的取值恰好相等，求事件 $C$ 发生的概率 $P (C)$ ；
（3）对（2）中的事件 $C$ , $C$ 表示 $C$ 的对立事件，判断 $P (C)$ 和 $P (C)$ 的大小关系，并说明理由。

如图，已知双曲线 $1, 2, . . . 2 n (n \in N^{+}, n \geq 2)$ 的右焦点 $a_{1}$ ,点 $a_{2}$ 分别在 $b_{1}$ 的两条渐近线上， $b_{1}$ 轴， $ξ = a_{2} - a_{1}, η = b_{1} - b_{2} / / n = 3$ ( $ξ$ 为坐标原点）.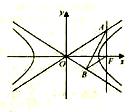

（1）求双曲线 $ξ$ 的方程；
（2）过 $η$ 上一点 $p (c)$ 的直线 $c$ 与直线 $p (c)$ 相交于点 $p (c)$ ，与直线 $x = \frac{3}{2}$ 相交于点 $N$ ，证明点 $P$ 在 $C$ 上移动时， $|\frac{M F}{N F}|$ 恒为定值，并求此定值.

如图，四棱锥 $P - A B C D$ 中， $A B C D$ 为矩形，平面 $P A D ⊥$ 平面 $A B C D$ .

(1)求证： $A B ⊥ P D$

(2)若 $∠ B P C = 90^{o}, P B = \sqrt{2}, P C = 2$ 问 $A B$ 为何值时，四棱锥 $P - A B C D$ 的体积最大？并求此时平面 $P B C$ 与平面 $D P C$ 夹角的余弦值.

已知函数 $f (x) = (x^{2} + b x + b) \sqrt{1 - 2 x} (b \in R)$ .
（1）当 $b = 4$ 时，求 $f (x)$ 的极值；
（2）若 $f (x)$ 在区间 $(0, \frac{1}{3})$ 上单调递增，求 $b$ 的取值范围.

已知首项都是1的两个数列 $\{a_{n}\}, \{b_{n}\}$ （ $b_{n} \neq 0, n \in N^{+}$ ），满足 $a_{n} b_{n + 1} - a_{n + 1} b_{n} + 2 b_{n + 1} b_{n} = 0$ .
（1）令 $c_{n} = \frac{a_{n}}{b_{n}}$ ，求数列 $\{c_{n}\}$ 的通项公式；
（2）若 $b_{n} = 3^{n - 1}$ ，求数列 $\{a_{n}\}$ 的前 $n$ 项和 $S_{n}$

试卷网试题网古诗词网作文网范文网