.(本小题满分12分)
已知直四棱柱ABCD—A′B′C′D′的底面是菱形，
，
E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2.
（1）求证：平面AEF⊥平面AA′C′C；
（2）求截面AEF与底面ABCD的夹角的大小.
已知：以点C (t, )(t∈R , t≠ 0)为圆心的圆与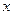
轴交于点O, A，与y轴交于点O, B，其中O为原点
（1）求△OAB的面积的值
（2）设直线y = –2x+4与圆C交于点M, N，若OM = ON，求圆C的方程
（本小题满分12分）
已知一圆C的圆心为（2，-1），且该圆被直线
：x-y-1="0" 截得的弦长为2
，
（1）求该圆的方程
（2）求过弦的两端点的切线方程
（本小题满分12分）
（本小题满分12分）
求下列各圆的标准方程：
（1）圆心在
上且过两点（2，0），（0，-4）
（2）圆心在直线
上，且与直线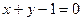
切于点（2，-1）
（本小题满分12分）
已知当k得值是多少时？
直线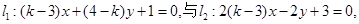
平
行
本小题满分10分）根据下列条件，求直线方程
（1）经过点A（3，0）且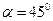
（2）经过点B（2，0），与C(0,-1)