.如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900.
M为AB的中点(1)求证:BC//平面PMD(2)求证:PC⊥BC;(3)求点A到平面PBC的距离.
如图,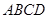 是边长为3的正方形,
是边长为3的正方形,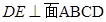 ,
, ,
, 与平面
与平面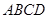 所成的角为
所成的角为 .
.
(1)求二面角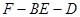 的的余弦值;
的的余弦值;
(2)设点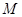 是线段
是线段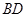 上一动点,试确定
上一动点,试确定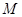 的位置,使得
的位置,使得 ,并证明你的结论.
,并证明你的结论.
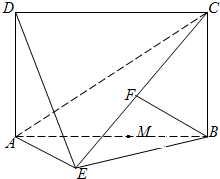
如图,四边形 为矩形,
为矩形,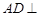 平面
平面 ,
, 为
为 上的点,且
上的点,且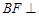 平面
平面 .
. 
(1)求三棱锥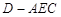 的体积;
的体积;
(2)设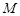 在线段
在线段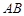 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点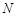 ,使得
,使得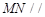 平面
平面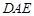 .
.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=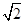 .
.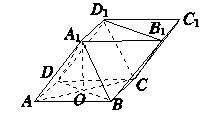
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
(1)按照画三视图的要求画出该多面体的俯视图;
(2)在所给直观图中连接BC′,求证:BC′∥面EFG.
如图,△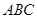 中,
中,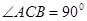 ,
,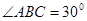 ,
,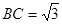 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心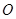 在边
在边 上,半圆与
上,半圆与 、
、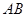 分别相切于点
分别相切于点 、
、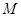 ,与
,与 交于点
交于点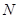 ),将△
),将△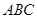 绕直线
绕直线 旋转一周得到一个旋转体。
旋转一周得到一个旋转体。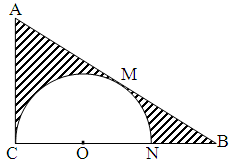
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.