(本小题满分12分)
从某校高三年级900名学生中随机抽取了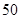
名测量身高，据测量被抽取的学生的身高全部介于
和
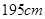之间，将测量结果按如下方式分成八组：第一组
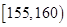,第二组
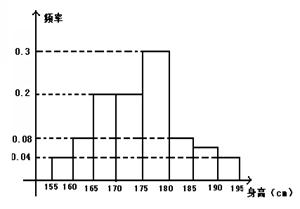
…第八组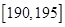
，右图是按上述分组方法得到的条形图．
（1）根据已知条件填写下面表格：
| 组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 样本数 |
|
|
|
|
|
|
|
|
（2）估计这所学校高三年级900名学生中，身高在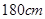
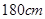以上（含）的人数；
（3）在样本中，若第二组有
人为男生，其余为女生，第七组有人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，用
表示实验小组中男同学的人数，求的分布列及期望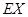
．
(13分)已知
.
(1)求
与
的夹角
;
(2)求
.
（本小题满分12分）设二次函数
满足下列条件：
①当
∈R时，
的最小值为0，且f (－1)=f(－－1)成立；
②当∈(0,5)时，≤≤2
+1恒成立。
（1）求
的值；
（2）求的解析式；
（3）求最大的实数m(m>1),使得存在实数t,只要当∈
时，就有
成立。
（本小题满分12分）
若函数y=f(x)是周期为2的偶函数,当x∈［2,3］时,f(x)=x－1,在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间［1,3］上,定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
（本小题满分12分）一列火车在平直的铁轨上匀速行驶，由于遇到紧急情况，火车以速度v(t)=5-t+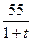
(单位：m/s)紧急刹车至停止。求：（1）从开始紧急刹车至火车完全停止所经过的时间；（2）紧急刹车后火车行驶的路程。
（本小题满分12分）
函数
的定义域为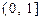
（
为实数）.
（1）当
时，求函数
的值域；
（2）若函数在定义域上是减函数，求的取值范围；
（3）函数在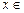
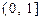上的最大值及最小值，并求出函数取最值时
的值