(13分)已知数列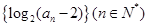 为等差数列,且
为等差数列,且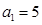 ,
,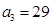 .
.
(1)求数列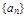 的通项公式;
的通项公式;
(2)对任意 ,
,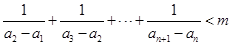 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;
恒成立的实数m是否存在最小值?如果存在,求出m的最小值; 如果不存在,说明理由.
如果不存在,说明理由.
在与角-2 010°终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)-720°~720°内的角.
已知角α的终边与-120°角的终边关于y轴对称.求α.
(本题10分)已知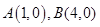 ,动点
,动点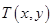 满足
满足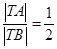 ,设动点
,设动点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线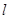 :
: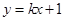 与曲线
与曲线 交于
交于 两点.(1)求曲线
两点.(1)求曲线 的方程;
的方程;
(2)若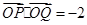 ,求实数
,求实数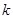 的值;
的值;
(3)过点 作直线
作直线 与
与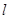 垂直,且直线
垂直,且直线 与曲线
与曲线 交于
交于 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.
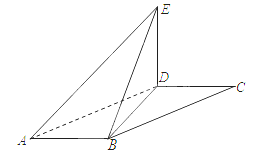
如图,已知四棱锥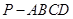 底面
底面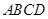 为菱形,
为菱形,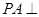 平面
平面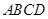 ,
,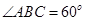 ,
, 分别是
分别是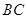 、
、 的中点.
的中点.
(1)证明:
(2)设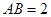 , 若
, 若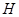 为线段
为线段 上的动点,
上的动点,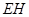 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为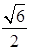 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.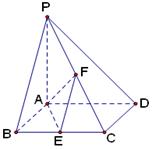
(本题满分10分) 如图,在平行四边形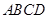 中,
中,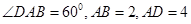 ,将
,将 沿
沿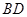 折起到
折起到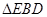 的位置,使平面
的位置,使平面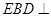 平面
平面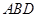 .
.
(1)求二面角E-AB-D的大小;
(2)求四面体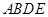 的表面积和体积.
的表面积和体积.