(本小题满分14分)
已知函数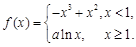
(1)若曲线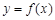 在
在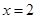 处的切线与直线
处的切线与直线 互相垂直,求
互相垂直,求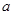 的值;
的值;
(2)若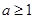 ,求
,求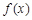 在
在 (
( 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(3)对任意给定的正实数 ,曲线
,曲线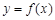 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在 轴上?
轴上?
设数列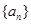 的前
的前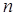 项和为
项和为 ,点
,点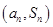 在直线
在直线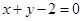 上,
上, .
.
(1)求证:数列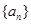 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)设直线 与函数
与函数 的图像交于点
的图像交于点 ,与函数
,与函数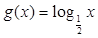 的图像交于点
的图像交于点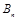 ,记
,记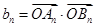 (其中
(其中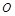 为坐标原点),求数列
为坐标原点),求数列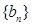 的前
的前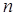 项和
项和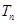 .
.
如图,三棱柱ABC﹣A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC,AA1= ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求三棱锥C1﹣ABB1的体积.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.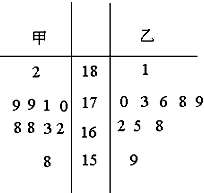
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
在 中,内角
中,内角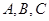 的对边分别为
的对边分别为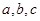 已知
已知 .
.
(1)求 的值;
的值;
(2)求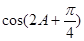 的值.
的值.
在数列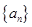 中,已知
中,已知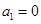 ,且对任意
,且对任意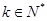 ,总有
,总有 成等差数列,其公差为
成等差数列,其公差为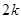 .
.
(Ⅰ)证明: ,
, ,
, 成等比数列;
成等比数列;
(Ⅱ)求数列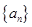 的通项公式;
的通项公式;
(Ⅲ)记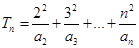 ,证明:
,证明: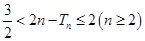 .
.