设数列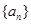 的前
的前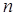 项和为
项和为 ,点
,点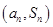 在直线
在直线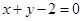 上,
上, .
.
(1)求证:数列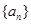 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)设直线 与函数
与函数 的图像交于点
的图像交于点 ,与函数
,与函数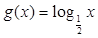 的图像交于点
的图像交于点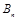 ,记
,记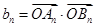 (其中
(其中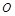 为坐标原点),求数列
为坐标原点),求数列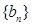 的前
的前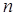 项和
项和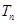 .
.
已知函数f(x)=(ax-a+2)·ex(其中a∈R).
(1)求f(x)在[0,2]上的最大值;
(2)若函数g(x)=a2x2-13ax-30,求a所能取到的最大正整数,使对任意x>0,都有2f′(x)>g(x)恒成立.
椭圆C: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .
.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
已知正项数列{an},{bn}满足:a1=3,a2=6,{bn}是等差数列,且对任意正整数n,都有bn, ,bn+1成等比数列.
,bn+1成等比数列.
(1)求数列{bn}的通项公式;
(2)求Sn= +
+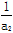 +…+
+…+ .
.
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4 ,AB=2
,AB=2 ,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
已知函数f(x)=sin +sin
+sin -2cos2x.
-2cos2x.
(1)求函数f(x)的值域及最小正周期;
(2)求函数y=f(x)的单调增区间.