(本题12分)高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
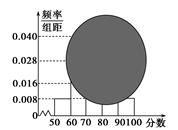
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)利用频率分布直方图估计本次测试成绩的中位数。
函数f(x)=|sin2x|+|cos2x|
(1)当x∈[0, ]时,求f(x)的取值范围;
]时,求f(x)的取值范围;
(2)我们知道,函数的性质通常指函数的定义域、值域、周期性、奇偶性、单调性等,请你探究函数f(x)的性质(本小题只需直接写出结论)
如图,已知正方形ABCD在直线MN的上方,边BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG,其中AE=2,记∠FEN=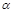 ,△EFC的面积为S.
,△EFC的面积为S.
(1)求S与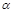 之间的函数关系;
之间的函数关系;
(2)当角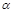 取何值时S最大?并求S的最大值。
取何值时S最大?并求S的最大值。
设函数f(x)=(sinax+cosax)2+2cos2ax(a>0)的最小正周期为 .
.
(1)求a的值;
(2)若函数y=F(x)的图象是由y=f(x)的图象向右平移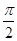 个单位长度得到,求y=F(x)的单调增区间.
个单位长度得到,求y=F(x)的单调增区间.
已知函数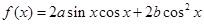 ,且
,且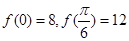 .
.
(1)求实数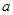 ,
, 的值;
的值;
(2)求函数 的最大值及取得最大值时
的最大值及取得最大值时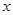 的值
的值
已知函数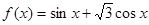 。
。
(1)求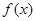 的周期和振幅;
的周期和振幅;
(2)在给出的方格纸上用五点作图法作出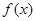 在一个周期内的图象。
在一个周期内的图象。