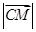在四棱锥P—ABCD中,底面ABCD是一直角梯形, ,
, 与底面成30°角。
与底面成30°角。
(1)若 为垂足,求证:
为垂足,求证: ;
;
(2)在(1)的条件下,求异面直线AE与CD所成角的余弦值;
(3)求平面PAB与平面PCD所成的锐二面角的正切值。
(本小题满分12分)学校生活区内建有一块矩形休闲区域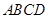 ,
, ,
, ,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路
,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路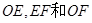 ,考虑到学校整体规划,要求
,考虑到学校整体规划,要求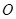 是
是 的中点,点
的中点,点 在边
在边 上,点
上,点 在边
在边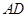 上,且
上,且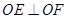 如图所示.
如图所示.
(1)设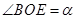 ,试将
,试将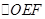 的周长
的周长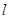 表示成
表示成 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
(本小题满分12分)设函数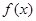 =
=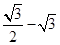
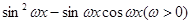 ,且
,且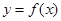 图象的一个对称中心到离它最近的对称轴的距离为
图象的一个对称中心到离它最近的对称轴的距离为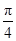 .
.
(1)求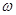 的值;
的值;
(2)求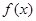 在区间
在区间 上的最大值和最小值,并求取得最大值与最小值时相应的
上的最大值和最小值,并求取得最大值与最小值时相应的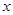 的值.
的值.
(本小题满分12分)设函数 (其中
(其中 ,
,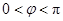 ,
,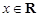 ).当
).当 时,
时,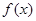 取得最小值
取得最小值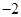 .
.
(1)求函数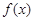 的解析式;
的解析式;
(2)求函数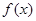 的单调递增区间.
的单调递增区间.
(本小题满分12分)已知向量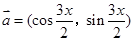 ,
,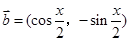 ,其中
,其中 .
.
(1)当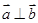 时,求
时,求 值的集合;
值的集合;
(2)当
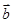 时,求
时,求 值的集合;
值的集合;
如图,在 中,
中,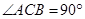 ,且
,且 ,点
,点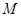 满足
满足 ,
,
(1)用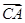 、
、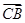 向量表示向量
向量表示向量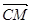 .
.
(2)求