如图,四棱锥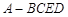 的底面
的底面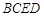 是直角梯形,
是直角梯形, ,
, ,
,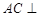 平面
平面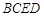 ,
, ,
,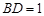 .
.
(1)求直线 与平面
与平面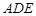 所成角的正弦值;
所成角的正弦值;
(2)在线段 上是否存在一点
上是否存在一点 ,使得异面直线
,使得异面直线 与
与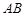 所成角余 弦值等
所成角余 弦值等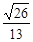 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.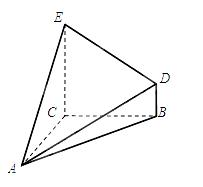
如图所示,有两条相交成 角的直路
角的直路 ,
,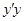 ,交点是
,交点是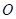 ,甲、乙分别在
,甲、乙分别在 ,
, 上,起初甲离
上,起初甲离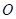 点
点 km,乙离
km,乙离 点
点 km,后来两人同时用每小时
km,后来两人同时用每小时 km的速度,甲沿
km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.
的方向步行.
⑴起初,两人的距离是多少?
⑵用包含 的式子表示
的式子表示 小时后两人的距离;
小时后两人的距离;
⑶什么时候两人的距离最短?
 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、b、c,若
、b、c,若 ,
, ,且
,且 .
.
(Ⅰ) 求角 ;
;
(Ⅱ) (只文科做)若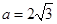 ,三角形面积
,三角形面积 ,求
,求 的值
的值
(只理科做)若 ,求2b+c的取值范围.
,求2b+c的取值范围.
已知函数 .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)求函数 在区间
在区间 上的值域.
上的值域.
已知数列{ }是等差数列,且
}是等差数列,且 =12,
=12, =27,
=27,
①求数列{ }的通项公式;②求数列{
}的通项公式;②求数列{ }的前
}的前 项和
项和
已知函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 。
。
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)如果当 ,且
,且 时,
时, ,求
,求 的取值范围
的取值范围