某市为组织开展第十五个“全国中小学安全教育日”活动，某中学举行了“全市中小学紧急疏散演练观摩会”．演练在一栋3层且每层楼有8间教室的教学楼中进行．教学楼共有3道门（两道大小相同的正门和一道侧门），在演练前，对这3道门进行了测试：当同时开启一正门和一道侧门时，半分钟内可以通过100名学生，若一道正门平均每分钟比一道侧门可多通过40名学生．
求平均每分钟一道正门和一道侧门各可以通过多少名学生?
测试中发现，紧急情况时因学生拥挤，出门的效率会降低20％，假设这栋教学楼每间教室平均有45名学生，在紧急情况下，全楼的学生能否在5分钟内通过这3道门安全撤离?并说明理由．
已知
，
，
（如图）．
是射线
上的动点（点与点
不重合），
是线段
的中点．
（1）设
，
的面积为
，求关于
的函数关系式，并写出自变量的取值范围；
（2）如果以线段
为直径的圆与以线段为
直径的圆外切，求线段
的长；
（3）连结
，交线段
于点
，如果以
为顶点的三角形与
相似，求线段的长．
某电子科技公司开发一种新产品．产品投产上市一年来，公司经历了由
初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）．公司
前12个月累积获得的利润y（万元）与销售时间第x（月）之间的函数关系（即前x个月的
利润总和y与x之间的关系）对应的点都在如图所示的图
象上．该图象是某二次函数
y=a(x-h)2+k图象的一部分，点A为抛物线的顶点，且点A，B，C的横坐标分别为4，10，
12，点A，B的纵
坐标分别为-16，20．
（1）求前12个月该公司累积获得的利润y（万元）与时间第x（月）之间的函数关系式；
（2）分别求出前9个月公司累积获得的利润和10月份一个月内所获得的利润；
（3）在前12个月中，哪个月该公司一个月内所获得的利润最多？最多利润是多少万元？
在平面上有且只有4个点，这4个点中有一个独特的性质：连结每两点可得到6条线段，这6条线段有且只有两种长度．我们把这四个点称作准等距点．例如正方形ABCD的四个顶点(如图1)，有AB=BC=CD=DA，AC=BD．其实满足这样性质的图形有很多，如图2中A、B、C、O四个点，满足AB=BC=CA，OA=OB=OC；如图3中A、B、C、O四个点，满足OA=OB=OC=BC，AB=AC．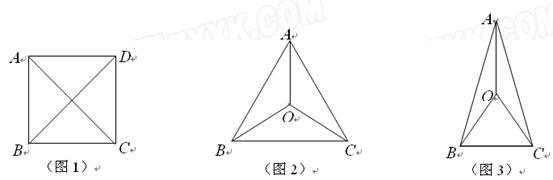
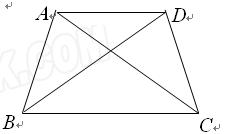
（1）如图，若等腰梯形ABCD的四个顶点是准等距点，且AD∥BC．
①写出相等的线段（不再添加字母）；
②求∠BCD的度数．
（2）请再画出一个四边形，使它的四个顶点为准等距点，并写出相等的线段．
在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸
货后返回．设汽车从甲地出发x(h)时，汽车与甲地的距离为y(km)，y与x的函数关系如图
所示．解答下列问题：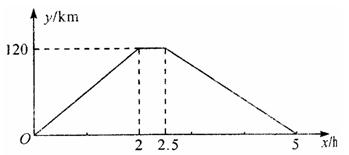
（1）这辆汽
车的往、返速度是否相同？请说明理由；
（2）求这辆汽车从甲地出发4h时与甲地的距离．
函数
的图象如图所示．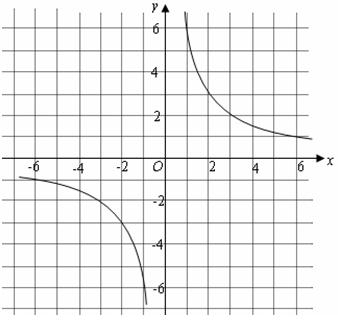
（1）
（
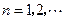）是第一象限内图象上的点，且
都是整数．求出所有的点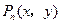
；
（2）若P（m，y1），Q(-3，y2)是函数图象上的两点，且y1> y2，求实数m的取值范围．