(本小题满分12分)已知数列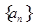 的前
的前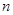 项和为
项和为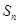 ,且
,且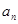 是
是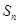 与2的等差中项,数列
与2的等差中项,数列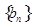 中,
中,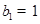 ,点
,点 在直线
在直线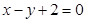 上.
上.
⑴求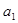 和
和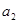 的值;
的值;
⑵求数列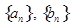 的通项
的通项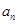 和
和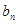 ;
;
⑶ 设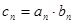 ,求数列
,求数列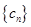 的前n项和
的前n项和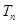 .
.
已知数列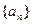 的前n项和为
的前n项和为
(1)求 的值,并猜想出数列
的值,并猜想出数列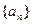 的通项公式
的通项公式
(2)设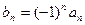 ,请利用(I)的结论,求数列
,请利用(I)的结论,求数列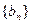 的前15项和
的前15项和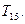
已知向量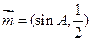 与
与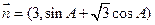 共线,其中A是△ABC的内角.
共线,其中A是△ABC的内角.
(1)求角 的大小;
的大小;
(2)若BC=2,求△ABC面积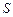 的最大值,并判断S取得最大值时△ABC的形状.
的最大值,并判断S取得最大值时△ABC的形状.
(本小题满分14分)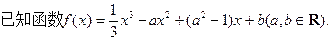
(Ⅰ)若x=1为f(x)的极值点,求a的值;
(Ⅱ)若y= f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0,求f(x)在区间[-2 ,4]上的最大值;
,4]上的最大值;
(Ⅲ )当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
)当a≠0时,若f(x)在区间(-1,1)上不单调,求a的取值范围.
(本小题 满分12
满分12 分)
分)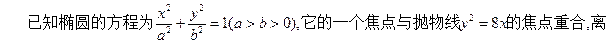
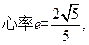 过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
(1)求椭圆的标准方程;
(2)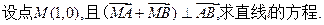
(本小题满分12分)
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足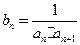 ,其前n项和为Sn.
,其前n项和为Sn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.