(本小题共15分)已知函数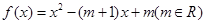 。
。
(1)若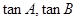 为
为 方程
方程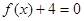 的两个实根,并且A,B为锐角,求m的取值范围;
的两个实根,并且A,B为锐角,求m的取值范围;
(2)对任意实数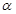 ,恒有
,恒有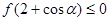 ,证明:
,证明: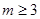 .
.
已知:公差不为零的等差数列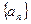 中,
中, 是其前
是其前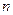 项和,且
项和,且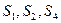 成等比数列.
成等比数列.
⑴求数列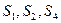 的公比
的公比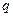 ;
;
⑵若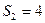 ,求等差数列
,求等差数列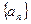 的通项公式.
的通项公式.
已知等比数列 各项为正数,
各项为正数,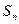 是其前
是其前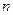 项和,且
项和,且
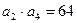 .
.
求 的公比
的公比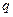 及
及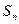 .
.
已知等差数列 中,
中, 是其前
是其前 项和,
项和, ,求:
,求: 及
及 .
.
为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
| 喜欢数学 |
不喜欢数学 |
总计 |
|
| 男 |
37 |
85 |
122 |
| 女 |
35 |
143 |
178 |
| 总计 |
72 |
228 |
300 |
由表中数据计算 ,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
某种产品表面进行腐蚀性试验,得到腐蚀深度 与腐蚀时间
与腐蚀时间 之间对应的一组数据:
之间对应的一组数据:
时间 |
深度 |
| 5 |
6 |
| 10 |
10 |
| 15 |
10 |
| 20 |
13 |
| 30 |
16 |
| 40 |
17 |
| 50 |
19 |
| 60 |
23 |
| 70 |
25 |
| 90 |
29 |
| 120 |
46 |
(1)试求腐蚀深度 对时间
对时间 的回归直线方程;
的回归直线方程;
(2)预测腐蚀时间为80 s时产品腐蚀的深度大约是多少?