(本小题满分14分)
已知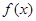 是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:
是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足: 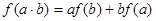 。
。
(1)求f(0),f(1)的值;
(2)判断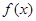 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(3)若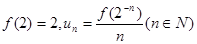 ,求数列{un}的前n项的和Sn 。
,求数列{un}的前n项的和Sn 。
函数f(x)= sin2x-
sin2x-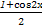 -
- .
.
(1)若x∈[ ,
, ],求函数f(x)的最值及对应的x的值.
],求函数f(x)的最值及对应的x的值.
(2)若不等式[f(x)-m]2<1在x∈[ ,
, ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
若向量m=(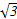 sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)=
sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)=
m·(m+n)+t的图象中,对称中心到对称轴的最小距离为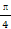 ,且当x∈[0,
,且当x∈[0, ]时,f(x)的最大值为1.
]时,f(x)的最大值为1.
(1)求函数f(x)的解析式.
(2)求函数f(x)的单调递增区间.
已知函数f(x)=sin sin(
sin(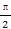 +
+ ).
).
(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈(0,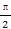 ),2f(2α)+4f(
),2f(2α)+4f(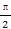 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为2,且当x= 时,f(x)的最大值为2.
时,f(x)的最大值为2.
(1)求f(x)的解析式.
(2)在闭区间[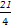 ,
, ]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ,x∈R)的图象的一部分如图所示.
,x∈R)的图象的一部分如图所示.
(1)求函数f(x)的解析式.
(2)当x∈[-6,- ]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
]时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.