(本题共3小题,每小题6分,满分18分)
已知函数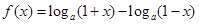

(1)讨论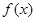 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式 的解集为
的解集为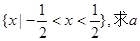 的值;
的值;
(3)设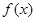 的反函数为
的反函数为 ,若关于
,若关于 的不等式
的不等式 R)有解,求
R)有解,求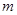 的取值范围.
的取值范围.
定义在R上的奇函数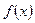 ,当
,当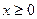 ,
,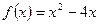
(1)作出函数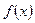 的图象
的图象
(2)求函数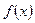 的表达式
的表达式
(3)求满足方程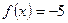 的解
的解
已知函数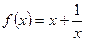
(1) 用函数单调性的定义证明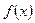 在区间
在区间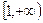 上为增函数
上为增函数
(2) 解不等式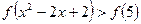
已知集合A=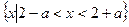 ,
,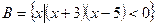
(1) 若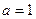 ,求
,求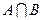
(2) 若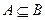 ,求
,求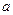 的取值范围
的取值范围
将十天干、十二地支按顺序依次排列,若 表示处于第
表示处于第 个位置的天干或地
个位置的天干或地
支,.
| 十天干 |
十二地支 |
|||||||||||||||||||||
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
 |
甲 |
乙 |
丙 |
丁 |
戊 |
己 |
庚 |
辛 |
壬 |
癸 |
子 |
丑 |
寅 |
卯 |
辰 |
巳 |
午 |
未 |
申 |
酉 |
戌 |
亥 |
如上表,即: ,
, .定义函数
.定义函数 .
.
(1)分别求 ,
, ,
,
(2) 2010年是庚寅年,我们也可以用
 的表示形式来表示该年,求
的表示形式来表示该年,求
的值
(本小题满分13分)已知函数 (
( ).
).
(1)若函数 有三个零点分别为
有三个零点分别为 ,且
,且 ,
, ,求函数
,求函数 的单调区间;
的单调区间;
(2)若 ,
, ,证明:函数
,证明:函数 在区间(0,2)内一定有极值点;
在区间(0,2)内一定有极值点;
(3)在(2)的条件下,若函数 的两个极值点之间的距离不小于
的两个极值点之间的距离不小于 ,求
,求 的取值范围.
的取值范围.