已知函数，令。（1）求函数的值域；（2）任取定义域内的5个自-优题课

已知函数，令。
（1）求函数的值域；
（2）任取定义域内的5个自变量，根据要求计算并填表；观察表中数据间的关系，猜想一个等式并给予证明；

						…
						…
						…

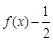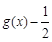（3）如图，已知在区间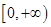的图像，请据此在该坐标系中补全函数在定义域内的图像，并在同一坐标系中作出函数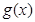的图像. 请说明你的作图依据.

科目数学题型解答题难度容易

知识点：平面向量的数量积高阶矩阵与特征向量

[选修4-5：不等式选讲]

已知 $f (x) = 2 |x| + |x - 2|$ ．

（1）求不等式 $f (x) \leq 6 - x$ 的解集；

（2）在直角坐标系 $x O y$ 中，求不等式组 $\{\begin{cases} f (x) \leq y \\ x + y - 6 \leq 0 \end{cases}$ 所确定的平面区域的面积．

[选修4-4：坐标系与参数方程]

在直角坐标系 $x O y$ 中，以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，曲线 $C_{1}$ 的极坐标方程为 $ρ = 2 \sin θ (\frac{π}{4} \leq θ \leq \frac{π}{2})$ ，曲线 $C_{2} : \{\begin{cases} x = 2 \cos α \\ y = 2 \sin α \end{cases}$ （ $α$ 为参数， $\frac{π}{2} < α < π$ ）．

（1）写出 $C_{1}$ 的直角坐标方程；

（2）若直线 $y = x + m$ 既与 $C_{1}$ 没有公共点，也与 $C_{2}$ 没有公共点、求 $m$ 的取值范围．

已知椭圆 $C : \frac{y^{2}}{a^{2}} + \frac{x^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{5}}{3}$ ，点 $A (- 2, 0)$ 在 $C$ 上．

（1）求 $C$ 的方程；

（2）过点 $(- 2, 3)$ 的直线交 $C$ 于点 $P$ ， $Q$ 两点，直线 $A P$ ， $A Q$ 与 $y$ 轴的交点分别为 $M$ ， $N$ ，证明：线段 $M N$ 的中点为定点．

已知函数 $f (x) = (\frac{1}{x} + a) \ln (1 + x)$ ．

（1）当 $a = - 1$ 时，求曲线 $y = f (x)$ 在点 $(1, f (1))$ 处的切线方程；

（2）若函数 $f (x)$ 在 $(0, + \infty)$ 单调递增，求 $a$ 的取值范围．

如图，在三棱锥 $P - A B C$ 中， $A B ⊥ B C$ ， $A B = 2$ ， $B C = 2 \sqrt{2}$ ， $P B = P C = \sqrt{6}$ ， $B P$ ， $A P$ ， $B C$ 的中点分别为 $D$ ， $E$ ， $O$ ，点 $F$ 在 $A C$ 上， $B F ⊥ A O$ ．

（1）求证： $E F ∥$ 平面 $A D O$ ；

（2）若 $∠ P O F = 120 °$ ，求三棱锥 $P - A B C$ 的体积．

试卷网试题网古诗词网作文网范文网