如图所示的长方体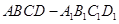 中,底面
中,底面 是边长为
是边长为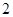 的正方形,
的正方形,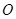 为
为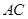 与
与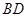 的交点,
的交点,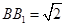 ,
, 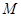 是线段
是线段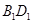 的中点.
的中点.
(1)求证: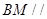 平面
平面 ;
;
(2)求三棱锥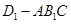 的体积.
的体积.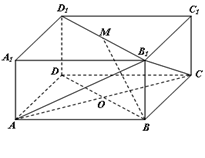
(本小题满分10分)袋中装有大小相同的黑球和白球共9个,从中任取2个都是白球的概率为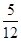 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量X的概率分布及数学期望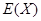 .
.
选修4—5:不等式选讲
设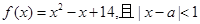 ,求证:
,求证: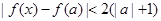 .
.
选修4—4:坐标系与参数方程
已知曲线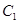 的极坐标方程为
的极坐标方程为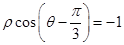 ,曲线
,曲线 的极坐标方程为
的极坐标方程为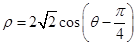 ,判断两曲线的位置关系.
,判断两曲线的位置关系.
选修4—2:矩阵与变换
已知矩阵 ,若矩阵
,若矩阵 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量为
,属于特征值1的一个特征向量为 .求矩阵
.求矩阵 的逆矩阵.
的逆矩阵.
选修4—1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 上的两点,
上的两点, ⊥
⊥ ,过点
,过点 作⊙
作⊙ 的切线FD交
的切线FD交 的延长线于点
的延长线于点 .连结
.连结 交
交 于点
于点 .
.
求证: .
.