已知数列 的前
的前 项和为
项和为 , 且
, 且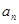 是
是 与2的等差中项,数列
与2的等差中项,数列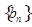 中,
中,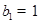 ,点
,点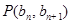 在直线
在直线 上。
上。
(Ⅰ) 求数列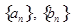 的通项公式
的通项公式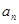 和
和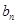 ;
;
(Ⅱ) 设 ,求数列
,求数列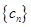 的前n项和
的前n项和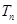 。
。
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;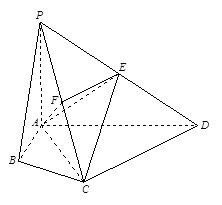
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5。同时投掷这两枚玩具一次,记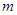 为两个朝下的面上的数字之和。
为两个朝下的面上的数字之和。
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)“m为奇数”的概率和“m为偶数”的概率是不是相等?证明你作出的结论。
如图,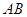 是底部
是底部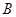 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物, 为塔的最高点.现需在塔对岸测出塔高
为塔的最高点.现需在塔对岸测出塔高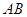 , 甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底
, 甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底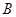 在同一水平面内的一条基线
在同一水平面内的一条基线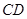 ,使
,使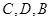 不在同一条直线上,测出
不在同一条直线上,测出 及
及 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),另外需在点
表示测得的数据),另外需在点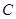 测得塔顶
测得塔顶 的仰角(用
的仰角(用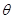 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高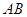 .乙同学的方法是:选一条水平基线
.乙同学的方法是:选一条水平基线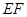 ,使
,使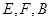 三点在同一条直线上.在
三点在同一条直线上.在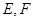 处分别测得塔顶
处分别测得塔顶 的仰角(分别用
的仰角(分别用 表示测得的数据)以及
表示测得的数据)以及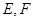 间的距离(用
间的距离(用 表示测得的数据),就可以求得塔高
表示测得的数据),就可以求得塔高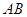 .请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时
.请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时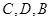 按顺时针方向标注,
按顺时针方向标注,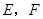 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高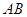 .
.
设不等式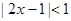 的解集是
的解集是 ,
,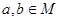 .
.
(I)试比较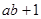 与
与 的大小;
的大小;
(II)设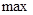 表示数集
表示数集 的最大数.
的最大数.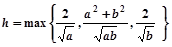 ,求证:
,求证: .
.
在平面直角坐标系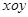 中,曲线
中,曲线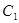 的参数方程为
的参数方程为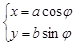 (
( ,
,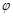 为参数),在以
为参数),在以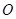 为极点,
为极点,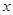 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线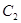 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线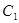 上的点
上的点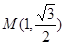 对应的参数
对应的参数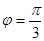 ,射线
,射线 与曲线
与曲线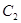 交于点
交于点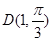 .
.
(I)求曲线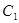 ,
,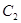 的方程;
的方程;
(II)若点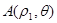 ,
, 在曲线
在曲线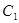 上,求
上,求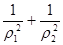 的值.
的值.