已知直线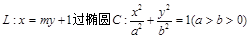 的右焦点F,且交椭圆C于A,B两点.
的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线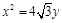 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对椭圆C,若直线L交y轴于点M,且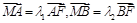 ,当m变化时,求
,当m变化时,求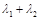 的值.
的值.
如图,函数f(x)=x+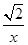 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.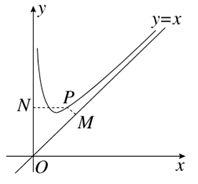
(1)证明:|PM|·|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
已知直线l经过直线2x+y-5=0与x-2y=0的交点.
(1)点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值.
已知直线l1:x+a2y+1=0和直线l2:(a2+1)x-by+3=0(a,b∈R).
(1)若l1∥l2,求b的取值范围;
(2)若l1⊥l2,求|ab|的最小值.
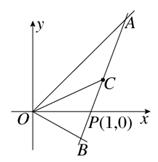
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=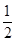 x上时,求直线AB的方程.
x上时,求直线AB的方程.