阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断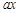 与
与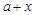 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出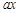 与
与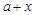 的差
的差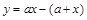 ,再
,再
说明y的符号即可.
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成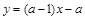 ,要判断y的符号可借助函数
,要判断y的符号可借助函数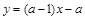 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且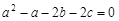 ,
, .
.(1)分别用含a的代数式表示4b,4c;
(2)说明a,b,c之间的大小关系.

计算:2×(-3)3-4×(-3)+15
我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101) ,(1011)
,(1011)  换算成十进制数为:
换算成十进制数为:
(101)  =1×2
=1×2 +0×2
+0×2 +1=4+0+1=5;(1011)
+1=4+0+1=5;(1011)  =1×2
=1×2 +0×2
+0×2 +1×2
+1×2 +1=11;
+1=11;
两个二进制数可以相加减,相加减时,将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似,应用“逢二进一”、“退一还二”的运算法则,如: (101)  +(11)
+(11)  ="(1000)"
="(1000)"  ;(110)
;(110)  +(11)
+(11)  ="(11)"
="(11)"  ,用竖式运算如右侧所示.(12分)
,用竖式运算如右侧所示.(12分)
(1)按此方式,将二进制(1001)2换算成十进制数的结果是 ▲ .
(2)计算:(10101)  +(111)
+(111)  = ▲ (结果仍用二进制数表示);
= ▲ (结果仍用二进制数表示);
(110010)  -(1111)
-(1111)  = ▲ (结果用十进制数表示).
= ▲ (结果用十进制数表示).
如图,已知OE平分∠AOC,OF平分∠BOC (12分)
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数。
(2)若∠AOC=x°,∠EOF=y°,∠BOC=60°,请用x 的代数式来表示y.
(3)如果∠AOC+∠EOF=210°,∠BOC=60°,则∠EOF是多少度?
剃须刀由刀片和刀架组成。某时期,甲、乙两厂家分别生产老式剃须刀(刀片不可更换)和新式剃须刀(刀片可更换),有关销售策略与售价等信息如下表所示:
某段时间内,甲厂家销售了8000把剃须刀,乙厂家销售的刀片数量是刀架数量的50倍,乙厂家获得的利润是甲的两倍,问这段时间内,乙销售了多少把刀架?多少片刀片?(10分)
| 老式剃须刀 |
新式剃须刀 |
||
| 刀架 |
刀片 |
||
| 售价 |
2.5(元/把) |
1 (元/把) |
0.55(元/片) |
| 成本 |
2 (元/把) |
6 (元/把) |
0.05(元/片) |