如图1，在△ABC中，∠ACB=90°，AC=3，BC=4，将△ABC绕顶点C顺时针旋转30°，得到△A′B′C．联结A′A、B′B，设△ACA′和△BCB′的面积分别为S△ACA′ 和S△BCB′．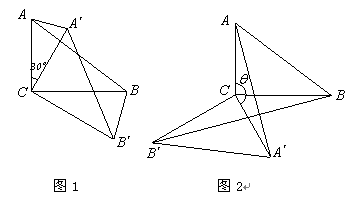
（1）直接写出S△ACA′ ︰S△BCB′ 的值 ；
（2）如图2，当旋转角为
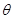（0°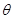＜＜180°）时，S△ACA′ 与S△BCB′ 的比值是否发生变化，若不变请证明；若改变，写出变化后的比值（可用含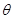的代数式表示）．
先化简，后求值：已知：[（x-2y）2-2y（2y-x）]÷2，其中x=1，y=2．
（1）解方程：3x2-27=0
（2）已知22x+1+4x=48，求x的值．
（本题14分）已知抛物线
（1）填空：抛物线的顶点坐标是（ ，），对称轴是 ；
（2）已知y轴上一点A（0，-2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点 N，使以点O、点A、点M、点N为顶点的四边形为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由．
（本题12分） 某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出400千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）当每千克涨价为多少元时，每天的盈利最多？最多是多少？
（2）若商场只要求保证每天的盈利为4420元，同时又可使顾客得到实惠，每千克应涨价为多少元？
（本题10分）如图，在⊙O中，弧AB=60°，AB=6，
（1）求圆的半径；
（2）求弧AB的长；
（3）求阴影部分的面积．