（本小题满分12分）某地区的海产品由A地运往B地，汽车货运公司和铁路货运公司均开办海产品运输业务。已知运输路程为120km，汽车和火车的速度分别为60km/h和100km/h，两货运公司的收费项目及收费标准如下表所示：
| 运输工具 |
运输费 （元/吨·千米） |
冷藏费 （元/吨·小时） |
过路费 （元） |
装卸及 管理费（元） |
| 汽车 |
2 |
5 |
200 |
0 |
| 火车 |
1.8 |
5 |
0 |
1600 |
注：“元/吨·千米”表示每吨货物每千米的运费；
“元/吨·小时”表示每吨货物每小时冷藏费。若该批发商待运的海产品有30吨，为节省运费，应选哪个货运公司？
若该批发商待运的海产品有60吨，他又该选哪个货运公司较为合算？
当该批发商有多少海产品时，无论选哪家都一样？
已知不等式组：
（1）求满足此不等式组的所有整数解；
（2）从此不等式的所所有整数解中任取一个数，它是偶数的概率是多少？
解方程组：
如图， 是一张锐角三角形的硬纸片． 是边 上的高， ， ．从这张硬纸片剪下一个长 是宽 的 倍的矩形 ．使它的一边 在 上，顶点 ， 分别在 ， 上． 与 的交点为 ．
（1）求证：
；
（2）求这个矩形
的周长．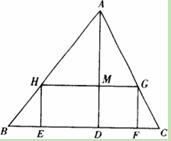
如图，在平面直角坐标系中，点A的坐标为（1，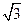
）
，△AOB的面积是．
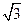（1）求点B的坐标；
（2）求过点A、O、B的抛物线的解析式；
（3）在（2）中抛物线的对称轴上是否存在点C，使△AOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；
（4）在（2）中x轴下方的抛物线上是否存在一点P，过点P作x轴的垂线，交直线AB于点D，线段OD把△AOB分成两个三角形．使其中一个三角形面积与四边形BPOD面积比为2：3？若存在，求出点P的坐标；若不存在，请说明理由．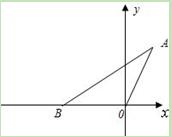
如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，AE=
ED，延长DB到点F，使FB=BD，连接AF．
（1）证明：△BDE∽△FDA；
（2）试判断直线AF与⊙O的位置关系，并给出证明．