(本小题满分12分)
经统计,某大型商场一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 |
0~5 |
6~10 |
11~15 |
16~20 |
21~25 |
25人以上 |
| 概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)求每天不超过20人排队结算的概率;
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,商场就需要增加结算窗口,试问该商场是否需要产加结算窗口?
长方体ABCD—A1B1C1D1(如右图所示),宽、长、高分别为3、4、5,现有一甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.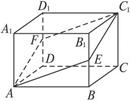
如右图P、Q分别是A1B1、BB1的四等分点,M、N分别是D1C1、CC1的中点.沿M→N→Q→P截去一部分,截去的几何体是什么?剩下的几何体也是吗?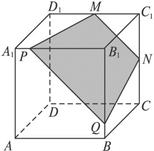
如图,已知二面角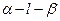 ,
,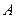 ,
,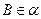 .
.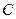 ,
,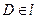 ,四边形
,四边形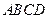 为矩形,
为矩形,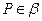 ,
,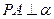 ,且
,且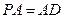 ,
,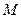 ,
,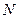 依次是
依次是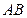 ,
,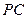 的中点.
的中点.
(1)求二面角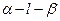 的大小;
的大小;
(2)求证: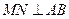 .
.
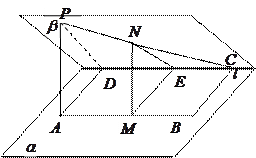 |
一木块如图所示,点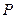 在平面
在平面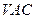 内,过点
内,过点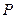 将木块锯开,使截面平行于直线
将木块锯开,使截面平行于直线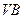 和
和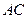 ,应该怎样画线?
,应该怎样画线?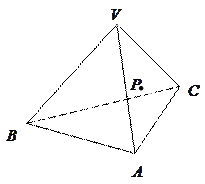
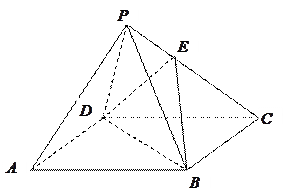
如图,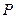 为正方形
为正方形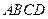 所在平面外一点,且
所在平面外一点,且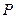 到正方形的四个顶点距离相等,
到正方形的四个顶点距离相等,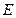 为
为 中点.求证:(1)
中点.求证:(1)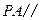 面
面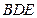 ;(2)面
;(2)面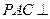 面
面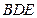 .
.
 |