本题共有3个小题,第1小题满分5分,第2小题满分6分,
第3小题满分7分.
对定义在区间 上的函数
上的函数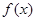 ,若存在闭区间
,若存在闭区间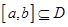 和常数
和常数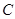 ,使得对任意的
,使得对任意的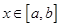 都有
都有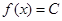 ,且对任意的
,且对任意的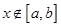 都有
都有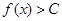 恒成立,则称函数
恒成立,则称函数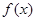 为区间
为区间 上的“U型”函数。
上的“U型”函数。
(1)求证:函数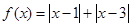 是
是 上的“U型”函数;
上的“U型”函数;
(2)设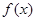 是(1)中的“U型”函数,若不等式
是(1)中的“U型”函数,若不等式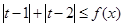 对一切的
对一切的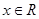 恒成立,
恒成立,
求实数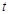 的取值范围;
的取值范围;
(3)若函数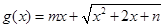 是区间
是区间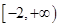 上的“U型”函数,求实数
上的“U型”函数,求实数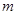 和
和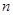 的值.
的值.
((本小题满分12分)
如图,四棱锥S—ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB= .
.
(Ⅰ)求面ASD与面BSC所成二面角的大小;
(Ⅱ)设棱SA的中点为M,求异面直线DM与
SB所成角的大小;
(Ⅲ)求点D到平面SBC的距离.
((本小题满分12分)
已知椭圆的中心在坐标原点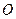 ,焦点在
,焦点在 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线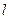 过
过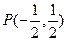 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,
求直线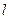 的方程.
的方程.
(本小题满分12分)
设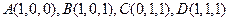 ,求直线AD与平面
,求直线AD与平面 的夹
的夹 角。
角。
已知命题 若
若 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围
的取值范围
(本小题 分)
分)
设 是数列
是数列 的前
的前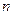 项和,点
项和,点
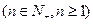 在直线
在直线 上.
上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,数列
,数列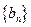 的前
的前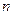 项和为
项和为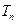 ,求使
,求使 的
的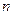 的最小值;
的最小值;
(Ⅲ)设正数数列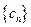 满足
满足 ,求数列
,求数列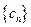 中的最大项.
中的最大项.