(本题满分14分，其中第1小题6分，第2小题8分)
为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用
(单位：万元)与隔热层厚度
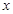(单位：cm)满足关系：
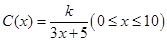，若不建隔热层，每年能源消耗费用为8万元．设
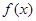为隔热层建造费用与20年的能源消耗费用之和．
(1)求
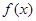的值及的表达式；
(2)隔热层修建多厚时，总费用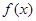达到最小，并求最小值．
甲乙两名工人生产的零件尺寸记成如图所示的茎叶图， 已知零件尺寸在区间[165，180]内的为合格品.(单位：mm)
（Ⅰ）求甲生产的零件尺寸的平均，乙生产的零件尺寸的中位数；
（Ⅱ）在乙生产的合格零件中任取2件，求至少有一件零件尺寸在中位数以上的概率.
已知正三棱柱ABC –A1B1C1中，AB = 2，AA1 =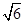
.
点F，E分别是边A1C1和侧棱BB1的中点.
（Ⅰ）证明：AC⊥平面BEF；
（Ⅱ）三棱锥F-AEC的体积.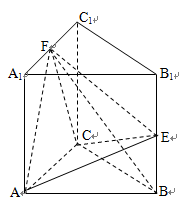
已知等比数列{an}的前n项和为Sn,A1="3," 且3S1 , 2S2 , S3成等差数列.
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log3an，求Tn=b1b2 - b2b3 + b3b4 - b4b5 + … + b2n-1b2n - b2nb2n+1
已知a , b , c∈R+，证明：
（Ⅰ）(A + b + c )(A2 + b2 + c2 ) ≤ 3(A3 + b3 +c3 )；
（Ⅱ）
.
已知曲线C的参数方程是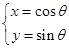
( θ为参数 )，以直角坐标系xoy的原点为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρ(cosθ+ sinθ) = 4
（Ⅰ）试求曲线C上任意点M到直线l的距离的最大值；
（Ⅱ）设P是l上的一点，射线OP交曲线C于R点，又点Q在射线OP上，且满足|OP|·|OQ|=|OR|2，当点P在直线l上移动时，试求动点Q的轨迹.