已知曲线C的参数方程是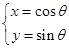 ( θ为参数 ),以直角坐标系xoy的原点为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ+ sinθ) = 4
( θ为参数 ),以直角坐标系xoy的原点为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(cosθ+ sinθ) = 4
(Ⅰ)试求曲线C上任意点M到直线l的距离的最大值;
(Ⅱ)设P是l上的一点,射线OP交曲线C于R点,又点Q在射线OP上,且满足|OP|·|OQ|=|OR|2,当点P在直线l上移动时,试求动点Q的轨迹.
(本小题满分13分)高三某班20名男生在一次体检中被平均分为两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示(如图).
(Ⅰ)求第一组学生身高的平均数和方差;
(Ⅱ)从身高超过180cm的五位同学中随机选出两位同学参加校篮球队集训,求这两位同学在同一小组的概率.
【参考公式:方差 ,其中
,其中 表示样本平均数】
表示样本平均数】
(本题共12分)对于每项均是正整数的数列 ,定义变换
,定义变换 ,
, 将数列
将数列 变换成数列
变换成数列
 .对于每项均是非负整数的数列
.对于每项均是非负整数的数列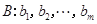 ,定义变换
,定义变换 ,
, 将数列
将数列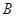 各项从大到小排列,然后去掉所有为零的项,得到数列
各项从大到小排列,然后去掉所有为零的项,得到数列 .又定义
.又定义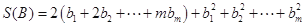 .设
.设 是每项均为正整数的有穷数列,令
是每项均为正整数的有穷数列,令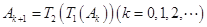 .
.
(Ⅰ)如果数列 为
为 ,写出数列
,写出数列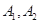 ;
;
(Ⅱ)对于每项均是正整数的有穷数列 ,证明
,证明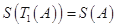 ;
;
(Ⅲ)证明:对于任意给定的每项均为正整数的有穷数列 ,存在正整数
,存在正整数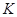 ,当
,当 时,
时,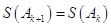 .
.
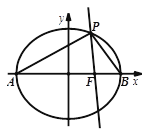
(本题共12分)已知椭圆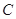 的中心在坐标原点,右焦点为
的中心在坐标原点,右焦点为 ,
, 是椭圆的左、右顶点,
是椭圆的左、右顶点, 是椭圆
是椭圆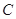 上异于
上异于 的动点,且
的动点,且 面积的最大值为
面积的最大值为 .
.
(Ⅰ)求椭圆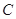 的方程;
的方程;
(Ⅱ)直线 与直线
与直线 交于点
交于点 .试判断以
.试判断以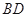 为直径的圆与直线
为直径的圆与直线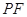 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(本题共12分)设函数 ,若对
,若对 均有
均有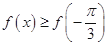 恒成立.
恒成立.
(Ⅰ)求实数 的值及函数
的值及函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在 中,
中,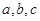 分别为内角
分别为内角 所对的边,且
所对的边,且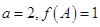 ,求
,求 的内切圆半径
的内切圆半径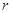 的最大值.
的最大值.
(本题共13分)如图,在多面体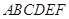 中,底面
中,底面 是边长为
是边长为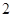 的菱形,
的菱形, ,四边形
,四边形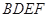 是矩形,平面
是矩形,平面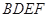 ⊥平面
⊥平面 ,
,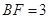 ,
,  是
是 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面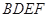 ;
;
(Ⅱ)求二面角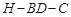 的大小.
的大小.