已知a , b , c∈R+,证明:
(Ⅰ)(A + b + c )(A2 + b2 + c2 ) ≤ 3(A3 + b3 +c3 );
(Ⅱ) .
.
已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,
D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥
P—ABC所成两部分的体积比.
在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.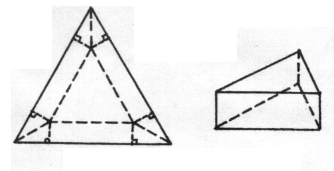
图①图②
如图a—l—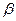 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在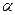 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在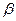 内,
内, ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=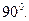
(I)求三棱锥D—ABC的体积;
(2)求二面角D—AC—B的大小;
(3)求异面直线AB、CD所成的角.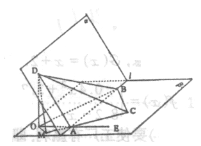
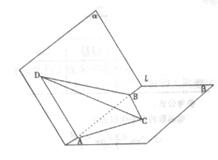
四棱锥P—ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°
如图,直角梯形ABCE中, ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0 。
。
(1)求直线AE与平面CDE所成的角;
(2)求证:MN//平面CDE。