本题共有2个小题,第1小题满分7分,
第2小题满分7分 .
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
,
已知 ,
, , 且
, 且 .
.
(1).求角 的大小;
的大小;
(2). 若 ,
, 面积为
面积为 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由.
已知椭圆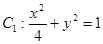 和动圆
和动圆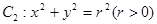 ,直线:
,直线: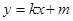 与
与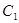 和
和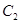 分别有唯一的公共点
分别有唯一的公共点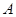 和
和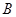 .
.
(Ⅰ)求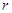 的取值范围;
的取值范围;
(Ⅱ)求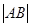 的最大值,并求此时圆
的最大值,并求此时圆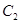 的方程.
的方程.
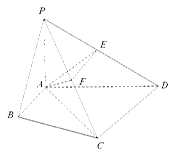
在四棱锥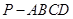 中,
中,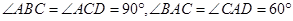 ,
,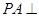 平面
平面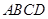 ,
,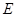 为
为 的中点,
的中点,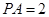 ,
,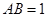 .
.
(Ⅰ)求四棱锥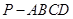 的体积
的体积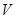 ;
;
(Ⅱ)若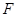 为
为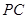 的中点,求证:平面
的中点,求证:平面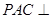 平面
平面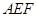 .
.
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,(阴影部分为破坏部分)其可见部分如下,据此解答如下问题: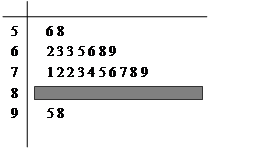

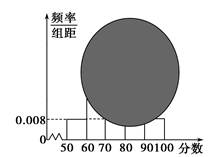
(Ⅰ)计算频率分布直方图中[80,90)间的矩形的高;
(Ⅱ)若要从分数在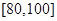 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在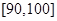 之间的概率;
之间的概率;
(Ⅲ)根据频率分布直方图估计这次测试的平均分.
在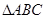 中,角
中,角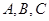 所对的边分别是
所对的边分别是 ,已知
,已知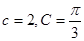 .
.
(1)若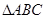 的面积等于
的面积等于 ,求
,求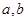 ;
;
(2)若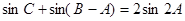 ,
,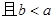 ,求
,求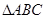 的面积.
的面积.
设不等式 的解集为
的解集为 ,
, .
.
(Ⅰ)证明: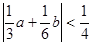 ;
;
(Ⅱ)比较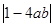 与
与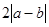 的大小,并说明理由.
的大小,并说明理由.