已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.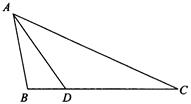
求证:△ABD∽△CBA;
若DE∥AB交AC于点E,请再写出另一个与△ABD相似的三角形,并直接写出DE的长.
化简求值:(1)2(a2b+ab2)-2(a2b-1)-3(ab2+1),其中a=-2,b=2;
(2)已知(x-5)2 +|m+2|=0,-2aby+1与4ab3是同类项,求代数式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
计算:(1)-(-1)3-(-1-3)×3÷(-4);(2)-8×(-2)4-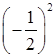 ×(-2)3+
×(-2)3+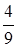 ×(-3)3.
×(-3)3.
如图, ABCD的两条对角线线交于O,且
ABCD的两条对角线线交于O,且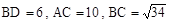 。
。
问:(1)AC、BD有什么位置关系?请说明理由;
(2)四边形ABCD是菱形吗?为什么?
在□ABCD中,点E、F分别在AB、CD上,FC=AE.四边形DEBF是平行四边形吗?说明理由. 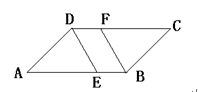
观察下列各式: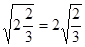 ,
, 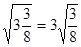 ,
, 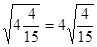
(1)找出规律,再继续写出下面的两个等式:
;。
(2)用含字母n(n≥2的整数)的等式表示以上的规律。