.(12分)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.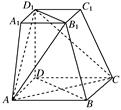
(本题满分12分)
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
如图所示,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=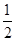 PD.
PD.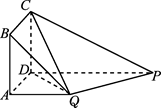
(1)证明:PQ⊥平面DCQ;
(2)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
| 男 |
女 |
总计 |
|
| 满意 |
50 |
30 |
80 |
| 不满意 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
(1)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关
注: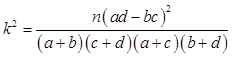
临界值表:
P( ) ) |
0.05 |
0.025 |
0.010 |
0.005 |
 |
3.841 |
5.024 |
6.635 |
7.879 |
在△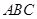 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知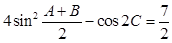 ,且
,且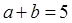 ,
, ,
,
求: (1) (2)△
(2)△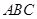 的面积.
的面积.
(本小题满分14分)
已知函数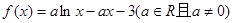 .
.
(Ⅰ) 求函数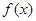 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点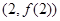 处的切线的倾斜角为
处的切线的倾斜角为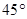 ,问:
,问: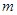 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数g(x)=x3 +x2
,函数g(x)=x3 +x2 在区间
在区间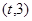 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数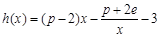 ,若在区间
,若在区间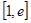 上至少存在一个
上至少存在一个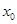 ,
,
使得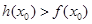 成立,试求实数
成立,试求实数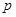 的取值范围.
的取值范围.