.某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果
如下表所示:
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用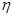 表示这两人休年假次数之和,记“函数
表示这两人休年假次数之和,记“函数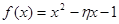 在区间
在区间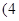 ,
,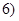 上有且只有一个零点”为事件
上有且只有一个零点”为事件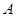 ,求事件
,求事件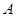 发生的概率
发生的概率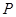 ;
;
(2)从该单位任选两名职工,用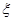 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量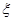 的分布列及数学期望
的分布列及数学期望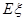 .
.
设平面内的向量 ,
, ,
, ,点
,点 是直线
是直线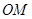 上的一个动点,且
上的一个动点,且 ,求
,求 的坐标及
的坐标及 的余弦值.
的余弦值.
在△ABC中,角A,B,C所对的边长分别是a,b,c.
(1)若sin C + sin(B-A)=" sin" 2A,试判断△ABC的形状;
(2)若△ABC的面积S = 3 ,且c =
,且c =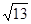 ,C =
,C = ,求a,b的值.
,求a,b的值.
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
在平面直角坐标系 中,点P到两点
中,点P到两点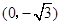 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
.
(Ⅰ)写出C的方程;
(Ⅱ)设直线 与C交于A,B两点.k为何值时
与C交于A,B两点.k为何值时

 ?此时
?此时 的值是多少?
的值是多少?
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是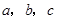 ,已知
,已知 ,
,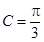 .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求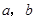 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.