(本题8分)在平面直角坐标系中,点A的坐标是(1,2).(1)请写出点A关于
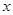 轴的对称点A’和关于
轴的对称点A’和关于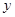 轴的对称点A,,的坐标;
轴的对称点A,,的坐标;(2)在(1)中连结A、 A//,在
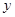 轴上找一点B,使得△ABA//为等边三角形,求出所有满足条件的B坐标;
轴上找一点B,使得△ABA//为等边三角形,求出所有满足条件的B坐标;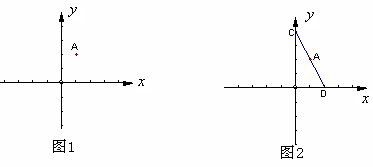
(3)过点A作一条直线交y轴于点C,交x轴于点D,点C的坐标为(0,4),点D的坐标为(2,0)若点P从点D出发,以1个单位每秒的速度向x轴负方向运动;点Q从点C出发,以2个单位每秒的速度向y轴负方向运动,经过多少时间,PQ的长度等于
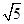 。
。
小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.观察与操作:

(1)他拼成如图②所示的正方形,根据四个小纸片的面积之和等于大正方形的面积,得到:a2+2ab+b2=(a+b)2,验证了完全平方公式;即:多项式 a2+2ab+b2分解因式后,其结果表示正方形的长(a+b)与宽(a+b)两个整式的积.
(2)当他拼成如图③所示的矩形,由面积相等又得到:a2+3ab+2b2=(a+2b)(a+b),即:多项式 a2+3ab+2b2分解因式后,其结果表示矩形的长(a+2b)与宽(a+b)两个整式的积.
问题解决:
(1)请你依照小刚的方法,利用拼图写出恒等式a2+4ab+3b2.(画图说明,并写出其结果)
(2)试猜想面积是2a2+5ab+3b2的矩形,其长与宽分别是多少?(画图说明,并写出其结果)
已知实数a、b满足(a+b)2=1,(a﹣b)2=25,求a2+b2+ab的值.
(A类)(1)已知x+y=1,求 x2+xy+
x2+xy+ y2的值;(2)已知10a=2,10b=3,求10a+b的值.
y2的值;(2)已知10a=2,10b=3,求10a+b的值.
(B类)(1)已知x2﹣3x+1=0,求x2+ 的值.(2)已知10a=20,102b=5,求10a﹣2b的值.
的值.(2)已知10a=20,102b=5,求10a﹣2b的值.
(C类)若x+y=2,x2+y2=4,求x2003+y2003的值.
求代数式5x2﹣4xy+y2+6x+25的最小值.
已知(2﹣a)(3﹣a)=5,试求(a﹣2)2+(3﹣a)2的值.