解方程: .
计算: .
【了解概念】
有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.

【理解运用】
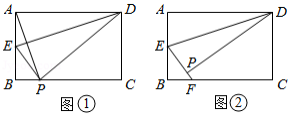
(1)如图①,对余四边形 中, , , ,连接 .若 ,求 的值;
(2)如图②,凸四边形 中, , ,当 时,判断四边形 是否为对余四边形.证明你的结论;
【拓展提升】
(3)在平面直角坐标系中,点 , , ,四边形 是对余四边形,点 在对余线 上,且位于 内部, .设 ,点 的纵坐标为 ,请直接写出 关于 的函数解析式.
已知抛物线 经过 , , 三点,对称轴是直线 .关于 的方程 有两个相等的实数根.
(1)求抛物线的解析式;
(2)若 ,试比较 与 的大小;
(3)若 , 两点在直线 的两侧,且 ,求 的取值范围.
矩形 中, , .将矩形折叠,使点 落在点 处,折痕为 .
(1)如图①,若点 恰好在边 上,连接 ,求 的值;
(2)如图②,若 是 的中点, 的延长线交 于点 ,求 的长.