有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字,函数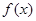 =
=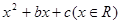 。
。
(Ⅰ)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数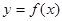 有零点的概率;
有零点的概率;
(Ⅱ) 求函数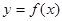 在区间(—3,+∞)是增函数的概率
在区间(—3,+∞)是增函数的概率
已知命题 :函数
:函数 的值域为
的值域为 ,命题
,命题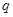 :方程
:方程 在
在 上有解,若命题“
上有解,若命题“ 或
或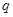 ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.
已知函数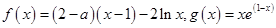 (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)
(1)当 时,求
时,求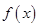 的单调区间;
的单调区间;
(2)若函数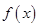 在
在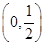 上无零点,求
上无零点,求 的最小值;
的最小值;
(3)若对任意的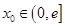 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得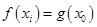 成立,求
成立,求 的取值范围.
的取值范围.
已知 ,当
,当 时,
时, .
.
(1)证明 ;
;
(2)若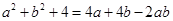 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 值的特点求出函数
值的特点求出函数 的表达式.
的表达式.
工厂生产某种产品,次品率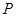 与日产量
与日产量 (万件)间的关系
(万件)间的关系 (
( 为常数,且
为常数,且 ),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元
),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元
(1)将日盈利额 (万元)表示为日产量
(万元)表示为日产量 (万件)的函数;
(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注: )
)
 中,设
中,设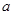 、
、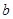 、
、 分别为角
分别为角 、
、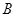 、
、 的对边,角
的对边,角 的平分线
的平分线 交
交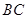 边于
边于 ,
, .
.
(1)求证: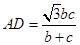 ;
;
(2)若 ,
,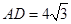 ,求其三边
,求其三边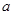 、
、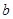 、
、 的值.
的值.