已知:双曲线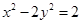 的左、右两个焦点分别为
的左、右两个焦点分别为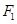 、
、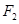 ,动点
,动点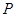 满足
满足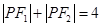 。
。
(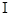 )求:动点
)求:动点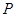 的轨迹
的轨迹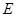 的方程;
的方程;
(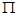 )若
)若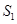 、
、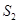 分别为(1)中曲线
分别为(1)中曲线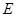 的左、右焦点,
的左、右焦点,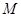 是曲线
是曲线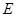 上的一个动点,
上的一个动点,
求: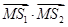 的最大值和最小值。
的最大值和最小值。
(本小题满分12分)已知首项都是1的两个数列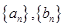 ,
, ,满足
,满足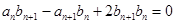 .
.
(1)令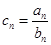 ,求数列
,求数列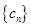 的通项公式;
的通项公式;
(2)若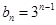 ,求数列
,求数列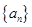 的前n项和
的前n项和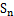
(本小题满分12分)已知函数 -
-
(1)求 的最小正周期及其对称中心;
的最小正周期及其对称中心;
(2)如果三角形ABC的三边a、b、c满足b2=ac,且边b所对角为x,试求x的范围及此时函数 的值域.
的值域.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
(本小题满分12分)
设数列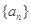 的前
的前 项和
项和 ,且
,且 成等差数列.
成等差数列.
(1)求数列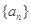 的通项公式;
的通项公式;
(2)记数列 的前n项和
的前n项和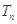 ,求得
,求得 成立的n的最小值.
成立的n的最小值.
(本小题满分10分)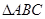 的内角A、B、C的对边分别为a、b、c,已知
的内角A、B、C的对边分别为a、b、c,已知 ,
, ,求B.
,求B.