(本题满分12分) 本题共有2个小题，第1小题满分6分，第2小题满分6分．
如图：三棱锥
中，
^底面
，若底面是边长为2的正三角形，且
与底面所成的角为
，若
是
的中点，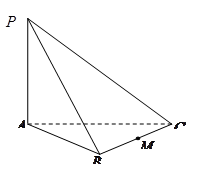
求：（1）三棱锥的体积；
（2）异面直线
与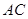
所成角的大小（结果用反三角函数值表示）.
探究：是否存在常数a、b、c使得等式1·22+2·32+…+n(n+1)2=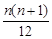
(an2+bn+c)
对对一切正自然数n均成立，若存在求出a、b、c，并证明；若不存在，请说明理由.
已知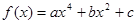
的图象经过点
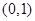，且在
处的切线方程是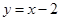
（1）求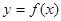
的解析式；
（2）求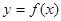的单调递增区间
(10分)已知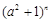
的展开式中各项系数之和等于
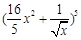的展开式的常数项，并且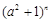的展开式中系数最大的项等于54，求
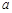的值．
(14分)设函数
，其中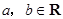
．
（Ⅰ）当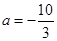
时，讨论函数
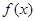的单调性；
（Ⅱ）若函数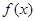仅在
处有极值，求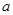
的取值范围；
（Ⅲ）若对于任意的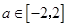
，不等式
在
上恒成立，求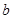
的取值范围．
(12分)在德国不来梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形展品，其中第一堆只有一层，就一个球，第2、3、4、…堆最底层（第一层）分别按下图方式固定摆放，从第二层开始每层的小球自然垒放在下一层之上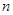，第
堆的第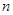层就放一个乒乓球，以
表示第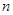堆的乒乓球总数.
（1）求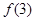
；
（2）求（用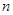表示）（可能用到的公式：
）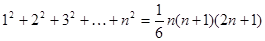